排容原理(Principle of Inclusion and Exclusion)(一)
國立高雄大學應用數學系游森棚副教授責任編輯
國立高雄大學應用數學系游森棚副教授責任編輯
排容原理( Principle of Inclusion and Exclusion, 簡稱PIE), 是高中排列組合的第三個, 也是最後一個基礎原理(前兩個是“乘法原理(Rule of Product)”與“加法原理” (Rule of Sum)) 亦有一些書按英文順序直譯為容斥原理(或許這是比較好的翻譯)。
排容原理中的‘排’ 是指“排除”, ‘容’是指“容納”。 基本上的想法就是“多退少補” — 多算的要排除, 少算的要加進來.。從原文亦可以清楚看出這個原理的精神。
高中數學的排容原理, 課堂上的實際教學不外乎從介紹下列式子開始:
高中數學的排容原理, 課堂上的實際教學不外乎從介紹下列式子開始:
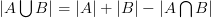 (1)
(1)
老師的講解都是用文氏圖(Venn diagram) 來說明的. 這是直觀而容易懂的好方法:
接著例題可能就是“國文及格有30 人, 數學及格有20 人, 兩科都及格有15人, 問至少一科及格有幾人?”. 緊接著必定會介紹三個集合的排容原理, 一樣會利用文氏圖來說明:
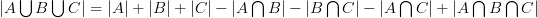 ,(2)
,(2)
高中的排容原理, 事實上教到這裡已經非常足夠了。但一些教師可能會接著介紹一般性的結果, 也許這樣講: “同理可證, 四個集合的排容原理如下:”
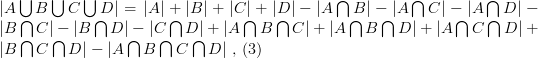
學生多半能從上述三個式子中看出規則, 老師最後就會說“一般來說, 有以下的排容原理:”
口頭上會加上說明: “一個一個加(所以一共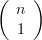 ) , 減去兩個兩個交集(所以一
) , 減去兩個兩個交集(所以一
共減去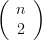 )項), 加回來三個三個交集(所以加回來
)項), 加回來三個三個交集(所以加回來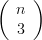 項), 再減去四個四個…”。
項), 再減去四個四個…”。
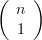 ) , 減去兩個兩個交集(所以一
) , 減去兩個兩個交集(所以一共減去
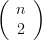 )項), 加回來三個三個交集(所以加回來
)項), 加回來三個三個交集(所以加回來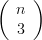 項), 再減去四個四個…”。
項), 再減去四個四個…”。
這樣的教學無可厚非, 師生都滿意, 皆大歡喜。
但是, 以上的教學過程卻有兩個很大的盲點一直被忽略。
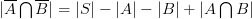 (5)
(5)
這當然也可以用文氏圖說明. 這個例題會是“全班有50 人, 國文及格有30 人, 數學及格有20 人, 兩科都及格有15 人, 問兩科都不及格有幾人?”
好, 問題來了. 到底(1) 式是排容原理, 還是(5) 式是排容原理?
筆者曾經對一群約五十位現任高中數學老師作調查, 答案是一面倒認為(1) 式才是排容原理. 但是並非如此!! 排容原理原始的精神是要算“這個條件也不成立,那個條件也不成立” 的方法數, 而不是算“至少有一個條件成立的方法數”. 因此嚴格說起來,
“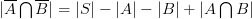 ”才是排容原理,
”才是排容原理,
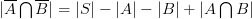 ”才是排容原理,
”才是排容原理,
而“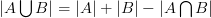 ”是“排容原理的對偶形式(dual form)”!
”是“排容原理的對偶形式(dual form)”!
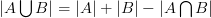 ”是“排容原理的對偶形式(dual form)”!
”是“排容原理的對偶形式(dual form)”!
第二個盲點, 三個集合的(2) 式可以用文氏圖說明是三個圓畫出來剛好把平面分成八塊, 但是, 如果讀者曾試著去畫四個圓交出來的文氏圖, 就會驚愕地發現, 四個圓最多只能把平面分成14 塊! 要用文氏圖說明, 必須要有16 個區域! 所以,
從三個集合的(2) 式到四個集合的(3) 式, 並不能“同理可證”!
因此證明四個集合以上的排容原理(或是對偶的排容原理), 並不是“同理可證”或“一般來說” 就可以矇過去的. 這是需要一點功夫的. 我們將在下一篇文章中討論。
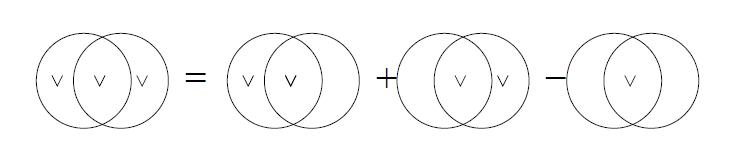

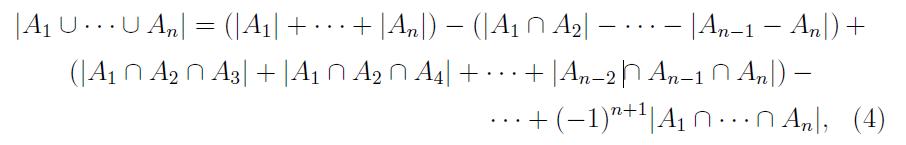
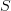 去減, 再於左式用笛摩根
去減, 再於左式用笛摩根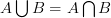 )後可以得到下式:
)後可以得到下式: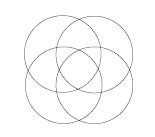
沒有留言:
張貼留言