以下問題,我於課堂上已說過,這裡純粹為同學留一個詳細記錄而已。
Applied mathematics (II) textbook Ex. 2(g) #2
A certain number,  , of persons sit down in a random arrangement on chairs labelled with their names. If
, of persons sit down in a random arrangement on chairs labelled with their names. If 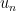 denotes the probability that all
denotes the probability that all  chairs are filled wrongly, write down the values of
chairs are filled wrongly, write down the values of 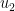 ,
,  ,
,  and
and  . Show that for
. Show that for 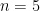 , the chance that more than one person is in his right chair slightly exceeds 0.25.
, the chance that more than one person is in his right chair slightly exceeds 0.25.
上述是一個經典問題:亂序(Derangement)的特例,一般問法是:
“n 個人入座,設每人有大會指定的坐位,但他們不清楚,亂坐,問他們完全『坐錯』的機會。”
“n 個人入座,設每人有大會指定的坐位,但他們不清楚,亂坐,問他們完全『坐錯』的機會。”
順著題意,列舉數例如下:
考慮  的情況,
的情況,
設正確排序為
1, 2
則亂序(即所謂『坐錯』)的情況是
2, 1
即是說亂序的情況有 1 個,或曰:亂序數 = 1;記之曰
故
設正確排序為
1, 2
則亂序(即所謂『坐錯』)的情況是
2, 1
即是說亂序的情況有 1 個,或曰:亂序數 = 1;記之曰
故
當  時,
時,
正確序:1, 2, 3
亂序:
2, 3, 1
3, 1, 2
即亂序數
故
正確序:1, 2, 3
亂序:
2, 3, 1
3, 1, 2
即亂序數
故
當  時,
時,
正確序:1, 2, 3, 4
亂序:
2, 1, 4, 3
2, 3, 4, 1
2, 4, 1, 3
3, 1, 4, 2
3, 4, 1, 2
3, 4, 2, 1
4, 1, 2, 3
4, 3, 1, 2
4, 3, 2, 1
即亂序數
故
正確序:1, 2, 3, 4
亂序:
2, 1, 4, 3
2, 3, 4, 1
2, 4, 1, 3
3, 1, 4, 2
3, 4, 1, 2
3, 4, 2, 1
4, 1, 2, 3
4, 3, 1, 2
4, 3, 2, 1
即亂序數
故
當  愈來愈大,要算數
愈來愈大,要算數  便愈來愈困難。但,若果我們知道以下關係:對
便愈來愈困難。但,若果我們知道以下關係:對  ,恆有
,恆有
我們便容易得出  了。
了。
則 。
。
則
問題是如何得到 (*) 這個遞迴關係?讓我以 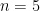 的情況說明。
的情況說明。
我們希望數算一下 5 個人『坐錯位』的情況有多少。
我們希望數算一下 5 個人『坐錯位』的情況有多少。
1 號位,要『坐錯』,我們可以『安排』阿 2,3,4,5 這 4 個人坐之。即 4 個可能性。
好了,假設阿 4 坐了 1 號位。讓我們看看 4 號位。這裡有以下 2 種『互斥』(exclusive) 的情況:
(情況 1) 阿 1 坐 4 號位。即是阿 1 和阿 4 交換了坐位。
(情況 2) 阿 1 不是坐 4 號位。
(情況 2) 阿 1 不是坐 4 號位。
好了,現在數算一下 (情況 1) 有多少可能性。
因為要 5 個人坐亂,已知阿 1 和阿 4 已交換坐,剩下的 3 個坐位 2,3,5 也要『坐亂』,即阿 2,3,5 要亂坐,由定義,3 人坐亂的亂序數為  ,即有 (情況 1) 共有
,即有 (情況 1) 共有  (= 2)種情況。
(= 2)種情況。
那麼 (情況 2) 有多少可能性呢?
答曰: 種。
種。
這裡,同學在堂上有疑問。 因為 (情況 2) 要求阿 1 不坐 4 號位;但, ,是 4 人坐亂的可能情況的數目,但 4 人坐亂,會否包括:『阿 1 坐了 4 號位』呢?如果包括,這個數算方法不是和 (情況 1) 有些『重疊』嗎?那麼它們便不是『互斥』事件了!
,是 4 人坐亂的可能情況的數目,但 4 人坐亂,會否包括:『阿 1 坐了 4 號位』呢?如果包括,這個數算方法不是和 (情況 1) 有些『重疊』嗎?那麼它們便不是『互斥』事件了!
嗯,這個可能是解說這問題的『難點』。
我們要數算 (情況 2) ,必要確保『阿 1 不坐 4 號位』;
那麼,讓我們把 4 號位『重新命名』為『1』號位,
即是,現在剩下了坐位 2,3,『1』,5,提供給阿 2,阿 3,阿 1,阿 5 坐下。
於是, 種情況,便已暗指『阿 1 不坐『1』號位』這個情況了。
種情況,便已暗指『阿 1 不坐『1』號位』這個情況了。
那麼,讓我們把 4 號位『重新命名』為『1』號位,
即是,現在剩下了坐位 2,3,『1』,5,提供給阿 2,阿 3,阿 1,阿 5 坐下。
於是,
於是,當阿 4 坐了 1 號位,共有  種坐亂的情況。
種坐亂的情況。
同理,阿 2, 阿 3, 阿 5, 也可安排坐 1 號位,分別也對應著 種坐亂的情況。
種坐亂的情況。
故 5 人坐亂的情況共有 種。
種。
同理,阿 2, 阿 3, 阿 5, 也可安排坐 1 號位,分別也對應著
故 5 人坐亂的情況共有
把問題一般化,考慮 n 人。設阿 k 坐了 1 號位(k  1),則 k 號位有以下兩種互斥情況:
1),則 k 號位有以下兩種互斥情況:
(情況 1) 阿 1 坐 k 號位。即是阿 1 和阿 k 交換了坐位。
(情況 2) 阿 1 不是坐 k 號位。
(情況 2) 阿 1 不是坐 k 號位。
因循上面類似的推論,
(情況 1) 共有 種(阿 k 和阿 1 交換,剩下 (n-2) 個位以提 n-2 人亂坐);
種(阿 k 和阿 1 交換,剩下 (n-2) 個位以提 n-2 人亂坐);
(情況 2) 共有 種(阿 k 坐了 1 號位,剩下 (n-1) 個位以提 n-1 人亂坐,特別地,阿 1 不能坐 k 號位)。
種(阿 k 坐了 1 號位,剩下 (n-1) 個位以提 n-1 人亂坐,特別地,阿 1 不能坐 k 號位)。
故當阿 k 坐了 1 號位,對應亂序總數為 ,
,
而 k 可以是 2,3,…,n (共 n – 1 種情況),於是有
(情況 1) 共有
(情況 2) 共有
故當阿 k 坐了 1 號位,對應亂序總數為
而 k 可以是 2,3,…,n (共 n – 1 種情況),於是有
對於  ,只要稍微推論,我們可得到
,只要稍微推論,我們可得到  的一般解如下:
的一般解如下:
要證明 (**),起碼有兩個方法。
(方法一)利用遞迴關係 (recurrence relation)
由 (*),得

(為何要考慮  ?頗自然的,我們想看看相鄰兩項究竟相差多少而已。)化簡,得
?頗自然的,我們想看看相鄰兩項究竟相差多少而已。)化簡,得
(***) 類似『reduction formula』,只要不斷運用它,index n 便可不斷下降 (reduced),即
=
=
… (inductively)
=
or
=
即
(****) 又是一種『reduction formula』,我們又可重覆使用之。
=
=
=
=
=
= …
(inductively)
=
+
+
+ …
+
=
即 (**),證畢。
(方法二)利用『容斥原理』(Inclusion-exclusion principle)
不詳談了,因為已經寫了很多廢話。簡而言之曰
設  為『阿 i 坐在 i 號位』這事件,則
為『阿 i 坐在 i 號位』這事件,則
=
=
再化簡,得 (**),證畢。
回答最初問題,
有了 的通解,立知
的通解,立知
有了
跟著的跟進問題是,當  很大時,
很大時,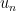 如何?怕你忘記,多給一個資料:
如何?怕你忘記,多給一個資料:
易知
這道題頗著名,相信最初的設定是『入錯信封』(未詳考究)。
沒有留言:
張貼留言